Quantitative Analysis and Simulation of Compressional Tectonics Based on Discrete Element Method (Tectonics and Mineralization)

2022年09月01日 Paper

Download：

Li Changsheng, Yin Hongwei, Xu Wenqiao, Wu Zhenyun, Guan Shuwei, Jia Dong, Ren Rong. Quantitative analysis and simulation of compaction structures based on discrete element method [J]. Geotectonica et Metallogenia, 2022, 46(04): 645-661.
The corresponding ZDEM script is provided later in the text.

The discrete element method (DEM) holds immense potential in the quantitative study of tectonic deformation, stress-strain relationships, and fracture prediction, making it one of the primary directions for future research in quantitative tectonic deformation studies.

Title

Quantitative Analysis and Simulation of Compressional Tectonics Based on Discrete Element Method

Authors

Changsheng Li^1,2,3,4, Hongwei Yin^3*, Wenqiao Xu³, Zhenyun Wu^{1, 2}, Shuwei Guan⁴, Dong Jia³, Rong Ren⁴

State Key Laboratory of Nuclear Resources and Environment, East China University of Technology, Nanchang, China
School of Earth Sciences, East China University of Technology, Nanchang, China
School of Earth Sciences and Engineering, Nanjing University, Nanjing, China
PetroChina Research Institute of Petroleum Exploration and Development, Beijing, China

Abstract

With advancements in discrete element theory and computer technology, DEM has been widely applied to tectonic simulations across various scales. Compared to traditional sandbox experiments, DEM allows for more precise control of experimental boundary conditions and quantitative analysis of the tectonic deformation process. This facilitates a deeper understanding of the influence of stratigraphic mechanical properties on tectonic deformation at the mesoscopic scale. This paper systematically elaborates on the quantitative analysis method for tectonic deformation based on DEM. Through a typical numerical simulation experiment of compressional tectonics using DEM, we modeled the formation process of tectonic structures under horizontal compression. The study analyzed the changes in stress and strain distribution, as well as the patterns of fracture generation during deformation, yielding the following insights:(1) The simulated tectonics are dominated by foreland-style imbricate thrust faults, with fault activity propagating sequentially from the compression end to regions farther away;(2) Fractures are closely related to fault formation, with the accumulation of numerous fractures in local areas acting as a trigger for fault development;(3) In the early stages of fault formation, material displacement within the fault is minimal, and the incremental increase in fractures is at its peak; in the later stages of fault activity, the incremental increase in fractures decreases;(4) Volumetric strain can characterize fracture types (tensile or compressive), while deformation strain can distinguish between forward and reverse thrust faults;(5) The magnitude of average stress is positively correlated with topographic relief, and the maximum shear stress continuously accumulates at the site of an impending new fault until the fault forms, after which the maximum shear stress dissipates, propagates forward, and accumulates at the next site of an impending fault. These findings demonstrate the significant potential of DEM in the quantitative study of tectonic deformation, stress-strain relationships, and fracture prediction.

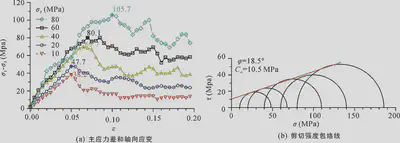
(a) Principal Stress Difference and Axial Strain;(b) Shear Strength Envelope

Figure 2: Biaxial Experiment Results

Figure 3: Initial Model

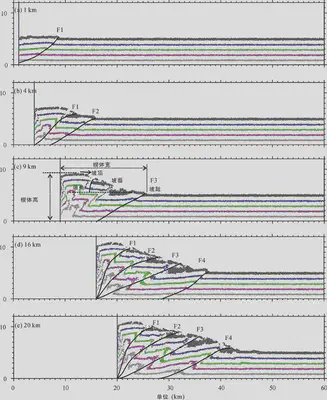
Figure 4: Structural Interpretation of the Wedge at Model Contraction of 1 km (a), 4 km (b), 9 km (c), 16 km (d), and 20 km (e)

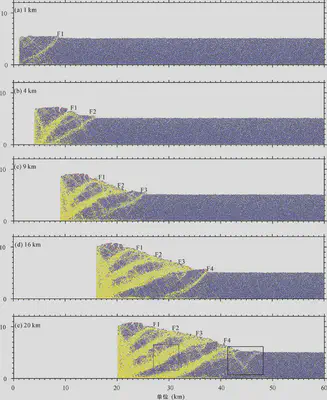
Figure 6: Bonded Force Chain Distribution at Contraction of 1 km (a), 4 km (b), 9 km (c), 16 km (d), and 20 km (e) (Blue represents bonded force chains, yellow represents unbonded contacts)

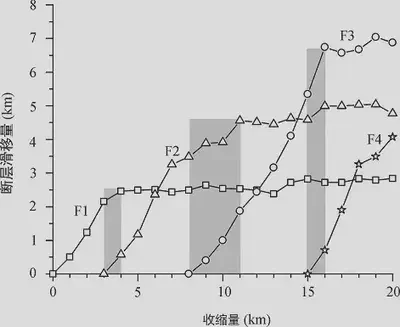
Figure 8: Fault Slip Curves as a Function of Contraction (Faults F1, F2, F3, and F4 as shown in Figure 4; fault slip values measured from the green layer)

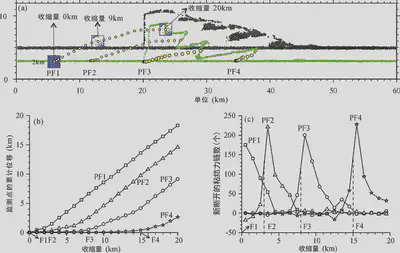
In Figure (a), four points are selected from four particles within faults F1, F2, F3, and F4 in the green marker layer. For clarity, the radii of these four particles are magnified threefold. The blue force chains represent bonded force chains within a 1 km radius around the monitoring points.

Figure 9: Motion Paths of Points PF1, PF2, PF3, and PF4 (a); Cumulative Displacement of Points PF1, PF2, PF3, and PF4 with Model Contraction (b); Number of Newly Broken Bonded Force Chains within a 1 km Radius Around Points PF1, PF2, PF3, and PF4 per 1 km of Model Contraction\(c)

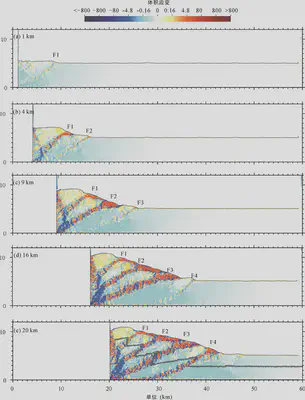
Here, blue indicates volumetric compression, red indicates volumetric expansion, and the intensity of the color represents the magnitude of volumetric change. In (e), the semi-transparent black layer is the marker layer.

Figure 10: Cumulative Volumetric Strain in the Model at Contraction of 1 km (a), 4 km (b), 9 km (c), 16 km (d), and 20 km (e)

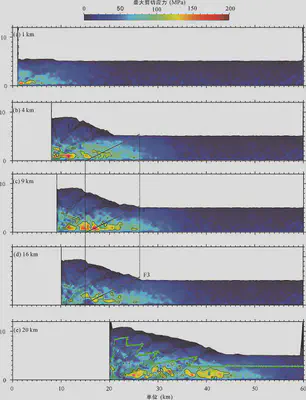
Black lines represent stress contours, and black dots indicate points with |deformation strain| > 4, marking fault locations. In Figure (e), the green layer is the marker layer.

Figure 15: Maximum Shear Stress Distribution at Contraction of 1 km (a), 4 km (b), 9 km (c), 16 km (d), and 20 km (e)

Acknowledgments

The numerical computations in this study were performed on the computing cluster at Nanjing University’s High-Performance Computing Center. The numerical simulation experiments were conducted using discrete element simulation software independently developed by our research group. For more examples of tectonic simulations, see https://geovbox.com. The strain calculation code used in this paper was adapted from scripts by Julia K. Morgan and Thomas Fournier of Rice University, to whom we express our gratitude. The source code for the wedge element measurement program is available at https://github.com/demsheng/Quantitative-wedge. Associate Professors Yu Yixin and Liu Zhina from China University of Petroleum (Beijing) provided thorough and professional reviews of this paper, offering constructive suggestions for improvement, for which we extend our special thanks.

ZDEM Script Code

Sedimentation Process.gen.py The content of is as follows:

######################################
# title: 基于离散元的挤压构造定量分析与模拟:1 沉积
# date: 2022-09-01
# authors: 李长圣
# E-mail: sheng0619@163.com
# ref: [李长圣,尹宏伟,徐雯峤,吴珍云,管树巍,贾 东,任 荣.基于离散元的挤压构造定量分析与模拟[J].大地构造与成矿学,2022,(46卷04):645-661.](https://doi.org/10.16539/j.ddgzyckx.2022.04.001) 
# more info, see www.geovbox.com
#######################################
start
set disk 0
BOX left 0.1 right 62000.0 bottom 1.0 height 20000.0 kn=4e10 ks=4e10 fric 0.00 
GLINE P1 (   1000.0 ,  1000.0 ) P2 (  61200.0 ,   1000.0 ) r 40.0 GROUP bom_wall
GLINE P1 (   1000.0 ,  1120.0 ) P2 (   1000.0 ,  19000.0 ) r 80.0 GROUP lef_wall
GLINE P1 (  61000.0 ,  1120.0 ) P2 (  61000.0 ,  19000.0 ) r 80.0 GROUP rig_wall

GEN num 200000, rad discrete 60.0 80.0,  x ( 1000 61000), y (1000 16000), COLOR black 
PROP den 2.5e3, fric 0.0, shear 2.9e9, poiss 0.2,  damp 0.4 hertz

prop color blue    range group bom_wall
prop color black   range group lef_wall
prop color black   range group rig_wall

fix x y  spin range group bom_wall
fix x y  spin range group lef_wall
fix x y  spin range group rig_wall

SET  DT 5e-2,  GRAVITY ( 0.0,  -9.8 )
PROP damp 0.4
DRAW INTERVAL 1000, bfill wall bondc ;,bid,bang  mesh, cforce

SET  stepbar  1000
SET  save    50000
set  print   1000
set  ps      1000

CYC 5000

del range x 1001 60999 y 7000 99999
CYC 5000
exp init6km_xyr.dat range x 1001.0 60999.0 y 1001.0 99999.0

del range x 1001 60999 y 6000 99999
CYC 5000
exp init5km_xyr.dat range x 1001.0 60999.0 y 1001.0 99999.0

stop

Compression Process.push.py The content of is as follows:

During the sedimentation process, particles are randomly generated, which may result in differences between the initial model and that described in the paper. Download the initial model from the paper:init5km_xyr.dat

######################################
# title: 基于离散元的挤压构造定量分析与模拟:2 挤压
# date: 2022-09-01
# authors: 李长圣
# E-mail: sheng0619@163.com
# ref: [李长圣,尹宏伟,徐雯峤,吴珍云,管树巍,贾 东,任 荣.基于离散元的挤压构造定量分析与模拟[J].大地构造与成矿学,2022,(46卷04):645-661.](https://doi.org/10.16539/j.ddgzyckx.2022.04.001) 
# more info, see www.geovbox.com
#######################################
load init5km_xyr.dat

set disk 0
BOX left 0.1 right 62000.0 bottom 1.0 height 20000.0 kn=4e10 ks=4e10 fric 0.00 
GLINE P1 (   1000.0 ,  1000.0 ) P2 (  61200.0 ,   1000.0 ) r 40.0 GROUP bom_wall
GLINE P1 (   1000.0 ,  1120.0 ) P2 (   1000.0 ,  19000.0 ) r 80.0 GROUP lef_wall
GLINE P1 (  61000.0 ,  1120.0 ) P2 (  61000.0 ,  19000.0 ) r 80.0 GROUP rig_wall

PROP color white den 2.5e3, fric 0.0, shear 2.9e9, poiss 0.2, hertz

prop color blue    range group bom_wall
prop color black   range group lef_wall
prop color black   range group rig_wall
fix x y   spin range group bom_wall
fix x y   spin range group lef_wall
fix x y   spin range group rig_wall

SET  DT 5e-2,  GRAVITY ( 0.0,  -9.8 )
PROP damp 0.4

SET  stepbar  1000
set  print    5000
set  ps       5000

prop   ebmod 2e8 gbmod 2e8 tstrength 1e7 sstrength 2e7 fric 0.3 range x 1001.0 60999.0 y 1001.0  9000.0
prop color mg     range x 1001.0 60999.0 y 1700.0  2000.0
prop color violet range x 1001.0 60999.0 y 2700.0  3000.0
prop color green  range x 1001.0 60999.0 y 3700.0  4000.0
prop color blue   range x 1001.0 60999.0 y 4700.0  5000.0
prop color black  range x 1001.0 60999.0 y 5700.0  9000.0

prop color blue   fric 0.3 range group lef_wall
prop color blue   fric 0.3 range group rig_wall
prop color red    fric 0.3 range group bom_wall

ini  xv 2.0, range group lef_wall
wall id 1, nodes (  500.0 , 2000.0 )  (    500.0 ,   3000.0 ), kn=0e3 ks=0e3 color black fric 0.0  xv  2.0
imple wall id 1 xmove 20000 print 1000.0 ps 1000.0 vtk 1000.0 sav 2000.0
stop

Translator: Bao Xianjun

Compressional Tectonics Stress and Strain Quantitative Analysis